Closed loop function

Analyze responses of a control system by using getIOTransfer to compute responses between various inputs and outputs of a closed-loop model of the system.

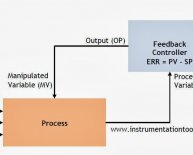
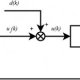
Consider the following control system.

Create a genss model of the system by specifying and connecting the numeric plant models G1 and G2, the tunable controllers C1 and C2, and the AnalysisPoint blocks X1 and X2 that mark potential loop-opening or signal injection sites.

G1 = tf(10, [1 10]); G2 = tf([1 2], [1 0.2 10]); C1 = tunablePID('C', 'pi'); C2 = tunableGain('G', 1); X1 = AnalysisPoint('X1'); X2 = AnalysisPoint('X2'); T = feedback(G1*feedback(G2*C2, X2)*C1, X1); T.InputName = 'r'; T.OutputName = 'y';

If you tuned the free parameters of this model (for example, using the tuning command systune), you might want to analyze the tuned system performance by examining various system responses.

For example, examine the response at the output, , to a disturbance injected at the point .

H1 = getIOTransfer(T, 'X1', 'y');

H1 represents the closed-loop response of the control system to a disturbance injected at the implicit input associated with the AnalysisPoint block X1, which is the location of :

H1 is a genss model that includes the tunable blocks of T. If you have tuned the free parameters of T, H1 allows you to validate the disturbance response of your tuned system. For example, you can use analysis commands such as bodeplot or stepplot to examine the the responses of H1. You can also use getValue to obtain the current value of H1, in which all the tunable blocks are evaluated to their current numeric values.

Similarly, examine the response at the output to a disturbance injected at the point .

H2 = getIOTransfer(T, 'X2', 'y');

You can also generate a two-input, one-output model representing the response of the control system to simultaneous disturbances at both and . To do so, provide getIOTransfer with a cell array that specifies the multiple input locations.