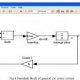
Closed loop control system diagram

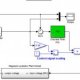
Signal flow graph of control system is further simplification of block diagram of control system. Here, the blocks of transfer function, summing symbols and take off points are eliminated by branches and nodes.The transfer function is referred as transmittance in signal flow graph. Let us take an example of equation y = Kx. This equation can be represented with block diagram as below The same equation can be represented by signal flow graph, where x is input variable node, y is output variable node and a is the transmittance of the branch connecting directly these two nodes.

Rules for Drawing Signal Flow Graph

1. The signal always travels along the branch towards the direction of indicated arrow in the branch.
2. The output signal of the branch is the product of transmittance and input signal of that branch.
3. Input signal at a node is summation of all the signals entering at that node.
4. Signals propagate through all the branches, leaving a node.

Simple Process of Calculating Expression of Transfer Function for Signal Flow Graph

• First, the input signal to be calculated at each node of the graph. The input signal to a node is summation of product of transmittance and the other end node variable of each of the branches arrowed towards the former node.
• Now by calculating input signal at all nodes will get numbers of equations which relating node variables and transmittance. More precisely, there will be one unique equation for each of the input variable node.
• By solving these equations we get, ultimate input and output of the entire signal flow graph of control system.
• Lastly by dividing inspiration of ultimate output to the expression of initial input we calculate the expiration of transfer function of that signal flow graph.

If P is the forward path transmittance between extreme input and output of a signal flow graph. L1, L 2…………………. loop transmittance of first, second, ……..loop of the graph. Then for first signal flow graph of control system, the overall transmittance between extreme input and output is Then for second signal flow graph of control system, the overall transmittance between extreme input and output is Here in the figure above, there are two parallel forward paths. Hence, overall transmittance of that signal flow graph of control system will be simple arithmetic sum of forward transmittance of these two parallel paths.

As the each of the parallel paths having one loop associated with it, the forward transmittances of these parallel paths are Therefore overall transmittance of the signal flow graph is

Mason's Gain Formula

The overall transmittance or gain of signal flow graph of control system is given by Mason’s Gain Formula and as per the formula the overall transmittance is Where, Pk is the forward path transmittance of kth in path from a specified input is known to an output node. In arresting P k no node should be encountered more than once. Δ is the graph determinant which involves closed loop transmittance and mutual interactions between non-touching loops. Δ = 1 - (sum of all individual loop transmittances) + (sum of loop transmittance products of all possible pair of non-touching loops) - (sum of loop transmittance products of all possible triplets of non-touching loops) + (……) - (……) Δ k is the factor associated with the concerned path and involves all closed loop in the graph which are isolated from the forward path under consideration. The path factor Δ k for the k th path is equal to the value of grab determinant of its signal flow graph which exist after erasing the K th path from the graph.